2013年のノーベル化学賞は、米国のマーティン・カープラス、マイケル・レビット、アリー・ウォーシェルの3氏に授与されることになりました。コンピュータを使って、大きくて複雑な分子の構造と反応を計算する手法を開発したことが授賞理由です。3人の業績はどのようなものか、それが今日の計算化学にどのように寄与しているのか、計算化学はどのように発展していくのかを、粒子系生物物理学研究チームの杉田有治チームリーダーにうかがいました。(文中、受賞者等の敬称略)
杉田ノーベル財団の発表では、授賞理由は「複雑な化学システムのためのマルチスケールモデルの開発に対して(for the development of multiscale models for complex chemical systems)」と書かれています。大きく、複雑な分子の構造と反応を計算するために、異なる分子モデルを混合した計算手法(マルチスケールモデル)が広く使われていますが、この方法を1970年代半ばまでに創始したことが評価されたのです。
計算化学におけるマルチスケールモデルは複数存在しますが、最もよく使われているのはQM/MM法です。この手法では、「量子力学 (Quantum Mechanics、QM) 法」と「分子力学 (Molecular Mechanics、MM) 法」という、2種類の計算法を組み合わせます。例えば、酵素(触媒作用をもつタンパク質)は数千~数万個もの原子からできていますが、そのうち最も重要な部分は、数十~数百個の原子からなる「活性部位」です。酵素はこの活性部位で化学反応を触媒するため、反応機構を解明するには、反応前、反応中、反応後の活性部位の原子配置と電子状態を、正確に予測することが必要です。そこで、活性部位だけをQMで詳細に計算し、周りの部分はMMでやや大ざっぱに計算しようというのがQM/MM法です。
QM法は、量子力学の理論に基づく計算法で、分子内の原子の配置と電子状態を精密に求めることができますが、膨大な計算量が必要です。一方、MM法は、分子内の原子の間に働くポテンシャルエネルギーを分子内のすべての原子について合計し、それが最小になる配置を求めます(図1)。この計算では、結合している原子間に働く力を古典的なバネ(調和振動子)やねじれ角エネルギーなどで近似し、離れた原子間の相互作用を原子どうしが引き合う力(ファンデルワールス相互作用)とクーロン力で近似します。これらをまとめて分子力場と呼びます。これによって、分子のエネルギーを計算するのに必要な演算量はQM法よりはるかに少なくなり、大きな分子を扱うことができます。QM/MM法は、両者のいいところを組み合わせるもので、計算量を抑えて必要な情報を得ることができます。

図1 レビットによる解説記事に掲載された分子力場の説明図(Reprinted by permission from Macmillan Publishers Ltd: Nature Structural Biology 8, 392 - 393 (2001))
分子力場のポテンシャルエネルギー(U)は、すべての原子の、原子間結合、結合角、ねじれ角、非結合原子対、部分電荷の相互作用を足し合わせたものである。
杉田QM法のほうが難しい理論に見えますが、量子力学の基礎は1920年代に確立されており、それを原子・分子の計算に応用する研究も早くから行われてきました。福井謙一先生を含め、この分野ではすでにノーベル賞受賞者が何人もいます。
一方、MM法を最初に開発したのはアリンジャーという人で、計算対象は小さな分子でした。これは1960年代のことで、QM法よりずっと遅いのです。ほぼ同時に、各国の研究者が同様の研究に取り組んでいましたが、中でも、イスラエルのワイツマン研究所にいたリフソンと、その研究室にいたレビット、ウォーシェルの3人は、1960年代後半にCFF(Consistent Force Field、矛盾のない力場)法という方法を開発しました。このプログラムは小さな分子から大きな分子まで計算できる、非常に優れたものでした。
ウォーシェルはCFF法のプログラムをもって、ハーバード大学のカープラスの研究室に行きました。カープラスは当時QM法の計算が専門でした。そして、2人のコラボレーションにより、1972年にMM法とQM法のカップリングが初めて実現したのです。このときは限られた形の分子にしか適用できなかったのですが、その後、ウォーシェルとレビットがタンパク質などを含むより一般的な分子に使えるように拡張しました。1976年のことです。
タンパク質はアミノ酸が鎖状にたくさんつながった高分子ですが、生理条件下では自発的に折れたたまって決まった立体構造をとります。しかし、この過程には時間がかかるため、当時の計算機上でMM法を用いてシミュレーションすることは不可能でした。レビットは、タンパク質の折りたたみ構造を計算する手法の開発にも取り組み、数個の原子の集まりを1個の疑似原子として扱う「粗視化」という方法を1975年に開発しました。これによって計算量は劇的に減少し、折りたたみ構造を計算することが可能になったのです。
全原子モデルと粗視化モデルを組み合わせた計算手法も、マルチスケール法の一つと考えることができます。現在では、生命科学だけでなく物質科学や材料化学などにおいても異なる粗視化モデルが開発されており、さまざまな用途に利用されています。図2と図3は、比較的最近行われたマルチスケールモデルを用いたシミュレーションの例です。
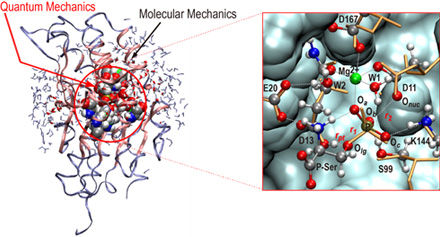
図2 酵素反応を理解するためのQM/MM計算の例(杉田TL提供)
脱リン酸化酵素の一種(ホスホセリンホスファターゼ)の反応を、活性部位はQM法で、周囲のペプチド鎖や水分子はMM法で計算したもの。こうした計算により、酵素の反応機構が詳しくわかり、人工酵素の設計や、創薬に発展させることができる。
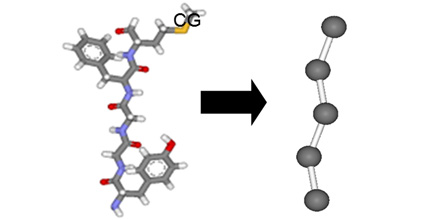
図3 「京」で用いられている粗視化モデル(京都大学高田彰二教授提供)
5つのアミノ酸からなるペプチドを全原子モデル(左)と粗視化モデル(右)で表現する。粗視化モデルでは、全原子モデルと比較して長時間の分子運動を少ない計算時間で計算することが可能になる。
杉田カープラスはMD法自体の創始者ではないのですが、1977年にタンパク質のMD計算に初めて成功しました。さらに、CHARMMというソフトウェアを開発し、タンパク質など生体高分子のMD法を発展させた人として有名です。ですので、私も第一報を聞いたときは、カープラスがついにMD法の開発に対してノーベル化学賞を受賞したのだと思いました。
MD法は、MM法で用いるポテンシャルエネルギーを微分することで各原子が受ける力を計算し、その力によって各原子がどのように運動するかを、ニュートンの運動方程式を解くことで調べるものです。MM法では分子内の原子のいちばん安定な配置を得るのに対し、MD法では分子が時々刻々、どのように形を変えていくかを計算することができます。タンパク質などの分子が反応するときには必ず動きを伴いますから、MD法のほうがより現実に近い構造状態を予測しているわけです。
カープラスやその門下生を含む多くの研究者の努力によって、MD法はさまざまな研究に使える方法として発展してきました。それにより、現在では、タンパク質の鎖が折りたたまれるようす、薬剤がタンパク質の活性部位に結合するかどうか、酵素反応がどのように進むかなどを予測できます。また、実験との連携により重要な情報が得られるようになりました。例えば、核磁気共鳴(NMR)法でタンパク質の構造を決定したり、X線結晶構造解析で得た構造をさらに精緻化したりするときにもMD法が使われています。
しかし、今回のノーベル賞では、1976年のQM/MM法の開発までが授賞対象となり、MD法の開発やその後の発展は対象となりませんでした。これには、カープラスも少しがっかりしているのではないかと想像します。今回は「MM法を開発し、応用可能な形に発展させたのは誰か」ということで受賞者が決まったと思われますが、このような研究を行ってきた研究者の数は多く、どのような切り口でとらえるかによって受賞者も変わった可能性があります。
杉田計算科学研究機構内では、私のチーム、プロセッサ研究チーム(泰地真弘人TL)、量子系分子科学研究チーム(中嶋隆人TL)などで、「京」でのシミュレーションを加速する計算手法やソフトウェアの開発が続けられています。さらに、HPCI戦略プログラム「分野1予測する生命科学・医療および創薬基盤」や「分野2新物質・エネルギー創成」、「分野4次世代ものづくり」などでも、「京」を用いたシミュレーションが活発に行われています。
例えば、私のチームでは、粗視化分子モデル、全原子モデル(MM法)、QM/MMモデルのすべてを連成する計算手法とソフトウェアの開発をめざしています。まだ開発は完全には終了していませんが、このような方法が完成すると、細胞膜に刺さるように存在する「膜タンパク質」の構造と機能の関係が計算科学によって解析できると期待しています。図4に示したイオンポンプは膜タンパク質の一種で、カルシウムイオンを、膜を隔てた濃度差に逆らって輸送します。このような複雑な化学システムを解明するには、膜タンパク質だけでなく、膜をつくっている脂質分子や周囲にある水分子も計算に含めなければなりません(図4)。
「分野1予測する生命科学・医療および創薬基盤」では、タンパク質の活性部位に薬剤がどのような強さで結合しているのかを、「京」を用いて計算しています。そのような計算は他の計算機上でも行われていますが、「京」を用いることにより、はるかに多くの薬剤候補について精度を落とさずに計算することが可能です。また、「分野2 新物質・エネルギー創成」でも、ウイルスまるごとを「京」の中で再現し、MD法を用いた計算を行うことで感染機構を解明する研究が進んでいます。
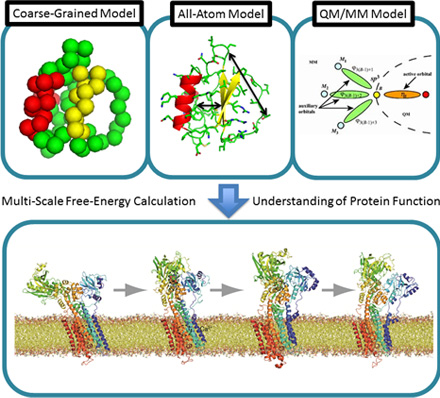
図4 カルシウムイオンポンプのイオン輸送機構の解明(杉田TL提供)
カルシウムイオンポンプは、細胞内にある小胞体の膜の外(つまり細胞質)から中へとカルシウムイオンを輸送する。小胞体の中のほうがカルシウムイオン濃度が高いので、濃度差に逆らう輸送となる。杉田TLは、粗視化分子モデル、全原子モデル(MM法)、QM/MMモデルのすべてを連成することによって膜タンパク質の動きを再現し、イオンポンプがカルシウムイオンを輸送するしくみを解明することをめざしている。
杉田例えば、膜タンパク質の構造と機能を計算科学のみで明らかにしようとすれば、「京」でも計算能力がまだまだ足りないと考えられています。イオンポンプがカルシウムイオンを輸送する1サイクルは(化学反応としては)長い時間がかかるため、これをMD法などで計算するには膨大な計算量が必要です。細胞内の環境を再現する計算や、さらに大きなウイルスの計算を長時間にわたって行おうとすれば、「京」の計算能力ですら、完全に十分とは言えないのです。また、創薬への応用をさらに現実的にしていくためにも、長時間のMD計算が必要です。QM/MM法とMD法と組み合わせて行う例も増えてきており、その場合にはさらに計算量が跳ね上がります。この分野の研究が、創薬や産業にほんとうの意味で応用されるようになるのは、「京」よりも計算能力の高いスパコンが登場したときかもしれません。
杉田どれだけ速いスパコンができても、「これでいい」と計算化学の研究者が満足することはないと思います。生体を含む自然現象は「複雑な化学システム」の上に成り立っています。我々が現在計算可能な化学現象はまだまだ限られていると思います。
しかし、計算化学は発展途上の学問分野です。今回の3人の受賞者の中で、特にカープラスには世界各地に非常にたくさんの弟子や孫弟子がいることで有名です。また、今回のノーベル賞は受けられなかったものの、この分野の確立に貢献した研究者もたくさんいますし、もちろん、その弟子や孫弟子もたくさんいるわけです。
計算化学のおもしろさは、新しいアルゴリズムや計算手法の開発によって、従来は解けなかった問題が解けるようになることです。そして、スパコンの演算能力は今後も著しく伸びると期待されますから、現在は非常に難しい問題が将来は簡単に解決できる可能性が高いと思います。実験でデータを得るのは難しいものですが、計算化学では必要な情報が揃っていれば再現性が非常に高いですし、一度解き方がわかれば類似の問題(例えばまったく別のタンパク質の問題)に応用することは簡単です。化学における実験の重要性は決して失われるものではありませんが、計算化学のさらなる発展により、将来的には多くの実験を計算で置き換えることが可能になると予想しています。そうなると、より本質的な問題に対して実験化学と計算化学の共同研究が活発に行われて、複雑な化学現象を解明できるようになり、さまざまな応用が実現するでしょう。


