スパコンのことば -その4-
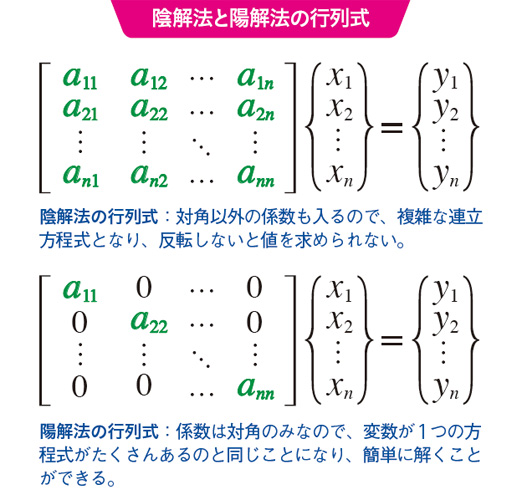
陰解法と陽解法
- Interview
- 超新星爆発を「京」で再現
- スパコンのことば
- -その4- 陰解法と陽解法
- 「京」まめ知識
- -vol.4- 京を待ちわびて
- 研究チーム紹介
- 牧野 淳一郎 チームリーダー
流体の時間発展、つまり、「ものの流れが時間とともにどう変化するか」のシミュレーションは、宇宙の進化や気象予測など、さまざまな分野の解析に登場します。実際には、もの(ニュートリノのような粒子や、大気の塊など)の位置の時間変化を表す微分方程式を立て、位置を示す座標xが、ある時間Δt後にどれだけ変化するか(変化量y)を繰り返し計算して時間発展を調べます。この計算を行うには、「陰解法」と「陽解法」という方法があります。
陽解法は、現在の位置xiからのΔt後の変化量yi+1を、Δt前から現在までの変化量yiをもとにして求める方法です。方程式は単純で、現在の情報があればすぐに計算できますが、Δtを小さくとらないとうまく計算できないという弱点があります。
一方、陰解法は、Δt後の変化量yi+1をいったん予測し、それが最初の微分方程式を満たすかを確かめてから変化量をきちんと求める方法です。先に行っては戻ることを繰り返すので、スパコンで解くべき方程式は複雑な行列式で表されることになり、それを解くには「行列式の反転」という計算量の大きな手続きが必要となります。しかし、予測を確かめながら進めるので、Δtを大きくとってもうまく計算することができます。
流体の時間発展の計算では、陰解法が使われるのが普通です。超新星爆発の際のニュートリノ輻射輸送のシミュレーションにも陰解法が使われてきましたが、今回、滝脇研究員は、「3次元計算では、そもそもΔtが小さいから、陽解法を使っても十分に計算できるのでは?」と気づき、実際に計算してみたところ、うまく計算することができました。陰解法での計算量は時間刻みの数nの2乗から3乗に比例しますが、陽解法ではnに比例するので計算量は激減し、さらに、エネルギー保存という条件も陰解法よりよく満たすといううれしい結果が得られました。
-
計算科学の世界No.9
2014年10月17日発行
- Interview
超新星爆発を「京」で再現 - スパコンのことば
-その4- 陰解法と陽解法 - 「京」まめ知識
-vol.4- 京を待ちわびて - 研究者に聞いてみよう!
牧野 淳一郎 チームリーダー - バックナンバー