Strongly correlated materials show great promise for next-generation electronic applications. In order to accelerate the development of functional strongly correlated materials, a reliable theory with good predictability is required. However, the strong interactions that take place in this class of materials do not allow us to apply the traditional band theory, which played a major role in the advance of today’s electronic technology based on semiconductors.
Consequently, we are developing large-scale numerical simulations for strongly correlated quantum systems, including strongly correlated materials, where the many-body interactions are essential to induce novel phenomena and properties. We are interested particularly in the quantum Monte Carlo method, the density matrix renormalization group method, and tensor network method to simulate not only the ground state but also the dynamics (thermodynamics, excitation dynamics, and real time dynamics) that occur between these systems and materials. We have established a platform for advanced research of strongly correlated quantum systems by developing state-of-the-art simulations.
Largest simulations ever for interacting Dirac electrons and universality of metal-insulator transitions
Understanding the nature of metal-insulator transitions induced by Coulomb repulsion between electrons has been one of the most fundamental issues in condensed matter physics. Considering the simplest model, i.e., a Hubbard model on the honeycomb lattice, we have analyzed the metal-insulator transition that occurs in this model when increasing the repulsive interaction. This model has attracted lots of interests because it is considered as one of the most effective models for graphene, where the non-interacting electrons exhibit the relativistic Dirac dispersion.
We have developed a quantum Monte Carlo software application to perform the largest ever simulations for the Hubbard model, which were performed on the K computer. Our highly optimized software allows us to treat 2,592 electrons, which is four times larger than the previous world record (648 electrons). Most importantly, we have shown that there is no intermediate phase between the metallic and insulating phases, thus the transition is continuous. In addition, we have determined with high accuracy the critical exponents that characterize this metal-insulator transition of interacting Dirac electrons. In the future, we will attempt even larger simulations to address more fundamental issues in modern condensed matter physics, which, until now, have not been considered possible.
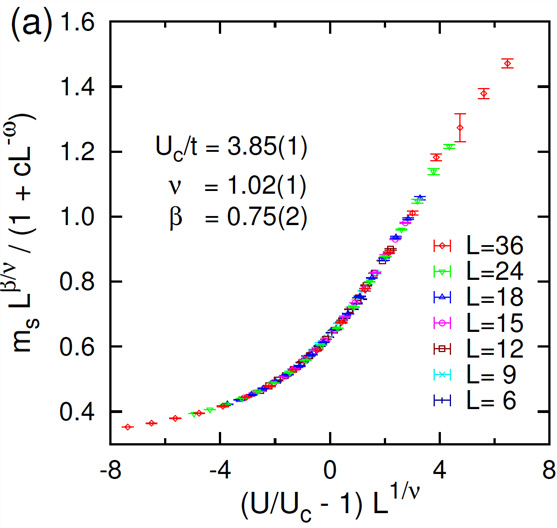
Metal-insulator transitions occurring for different system sizes (2L2) follow the universal function. The exponents (βandν) in this function characterize the transitions.





