A supercomputer makes it possible to handle tremendously large amounts of data. Many phenomena in the natural and social world change under certain regularities. A lot of this regularity can be expressed in equations. By rewriting these equations into programs and calculating tremendously by a computer, it is possible to arrive at solutions we have never obtained.

Studies aimed at resolving phenomena through calculations rather than experiments are called computational science, and programs for this purpose are called applications. Advanced technologies and a great deal of knowledge are required to write programs so as to maximize the performance of the K Computer.

Massively parallelization of applications on the K computer

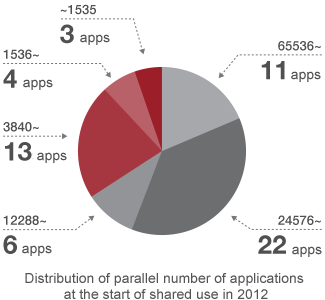
One of the significant characteristics of the K computer is a very large parallel number by 82,944 CPUs. Such a large number may cause an imbalanced operation between CPUs and/or increase communication traffic. In the former case, for example, a one-second CPU delay causes approximately 80,000-fold latency, which is equivalent to 22 hours. In the latter case, it takes longer to obtain results due to the significantly longer time needed for communications.

To overcome these problems and make massively parallel applications, we have provided the K computer resources and technical support since we started shared use, and improve the K computer whenever system problems arise. By these activities 39 applications have been successfully prepared to have sufficient performance on more than 10,000 parallel when starting the shared use.

High performance applications with the K computer

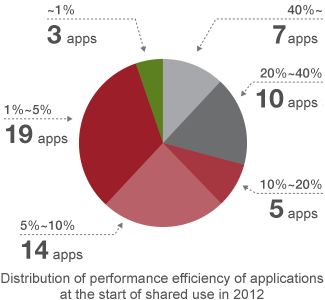
Application efficiency at the start of shared use

As well as other scalar computer, a data transmission capacity from memory of the K computer is not sufficient for its computational performance. Therefore, it is said to be relatively difficult to achieve high performance in some applications for example fluid simulation and structural analysis that require many data for a computation. To overcome such problems, we have applied performance improvement methods such as calculation order changing to enable repeat use of the same data on a cache memory. Then 17 applications performance achieved more than 20% of the peak performance of the K computer when starting the shared use.

 

Applications classified by method

Target	Method	Equation	Summary
Electrons (molecules, crystals)	Molecular Orbital Method (MO)	Hartree-Fock Method	This is a method of calculating quantum state of an electron by approximating an electron in a hydrogen atom, with which chemical reactions, shapes, and characteristics of a molecule can be calculated.
	Density Functional Theory (DFT)	Cahn–Hilliard Equation	This is a method of calculating quantum phenomena by approximating as electron motion in a charge distribution, with which chemical bonds and device characteristics can be calculated.
Magnetism, electrons	Monte Carlo Method (MC)	Hubbard Model, Ising Model, Detailed Balance Conditions	This is a method of sampling and statistically processing quantum phenomena of probabilistic motion. This can also be used for optimization, and can calculate device characteristics.
	Exact Diagonalization Method (ED) & Density Matrix Renormalization Group Method (DMRG)	Hubbard Model, Ising Model	These methods are for treating of quantum phenomena such as magnetism, as diagonalization problem of a Hamiltonian matrix, and can calculate device characteristics.
Objects (molecules, atoms, stars, plasmas)	Particle Method (MD, SPH，PIC)	Newton’s Equation	This is a method of estimating positions and velocities from forces applied to many objects, such as gravity and electrostatic force. It is possible to calculate density fluctuations from position information, and temperatures and pressures from velocity distributions. The SPH method has smoothness by further approximation of objects, and the PIC method is used to calculate force with a special mesh.
Fluids, structures (weather, oceans, earthquakes)	Finite Difference Method (FDM)	Navier-Stokes Equation, Hooke’s Law, Poisson’s Equation	This is a method of finding the motion of continuum as a change in volume on a mesh, with which fluxes and deformations can be calculated.
	Finite Element Method (FEM)		This is a method of estimating the motion of continuum on a mesh using highly interpolation. It is capable for using an unstructured mesh and possible to calculate deformation, stress concentration, flow rates and the motion of vortices.
	Boundary Element Method (BEM)		This is a method of solving equations of continuum by transforming the equations into formulae only on a boundary. Although it is possible to decrease calculations, more communications should be necessary.
	Finite Volume Method (FVM)		This is a method of calculating approximate solutions for the motion of continuum with a mesh. It is possible to adapt to various shapes, but is thought to be difficult to improve accuracy.